Pengertian deret dan aritmatika

Pengertian Barisan dan Deret Aritmetika

Dalam matematika, barisan dan deret aritmetika atau dikenal sebagai barisan dan deret hitung adalah barisan yang mempunyai pola tertentu, yakni selisih dua suku berturutan sama dan tetap. Dengan kata lain, setiap suku (kecuali suku pertama) pada barisan aritmetika diperoleh dari suku sebelumnya dengan menambah bilangan tetap, misalnya:

$3$ , $5$ , $7$ , $9$ , $11$ , $13$ , $\dots$ .

Barisan aritmetika ini dapat dinyatakan dengan rumus sebagai berikut.

$a$ , $a+b$ , $a+2b$ , $a+3b$ , $\dots.$

Selanjutnya, sebagaimana disadur dari buku berjudul Matematika SMK 2: Kelompok Bisnis dan Manajemen yang diterbitkan oleh Grasindo, barisan aritmetika adalah suatu baris di mana nilai pada masing-masing sukunya diperoleh dari suku sebelumnya lewat penjumlahan atau pengurangan dengan suatu bilangan b.

Lebih lanjut, selisih antara nilai suku-suku saling berdekatan dan selalu sama, yaitu b. Misalnya:

Un – U(n-1) = b

Sebagai contoh baris 1, 3, 5, 7, 9, merupakan baris aritmetika dengan nilai:

b = (9 – 7) = (7 – 5) = (5 – 3) = (3 – 1) = 2

Sementara itu, deret aritmetika adalah suatu penjumlahan antar suku-suku dari sebuah barisan aritmetika. Untuk penjumlahan dari suku-suku pertama hingga suku ke-n barisan aritmetika tersebut bisa dihitung sebagai:

Sn = U1 + U2 + U3 + …. + U(n-1)

atau

Sn = a + (a + b) + (a + 2b) + …. + (a + (n – 2)b) + (a + (n – 1)b)

Apabila yang diketahui hanya nilai a, suku pertama serta nilainya merupakan suku ke-n, jadi nilai deret aritmetikanya adalah:

Sn = n/2(a + Un))

Suku

Suku Barisan Aritmetika

Misal $a_{n}$ adalah suku barisan ke- $n$ , maka

$\ a_{n}=a+(n-1)b$ .

Bukti
Kita mulai mengurutkannya dari suku $a_{1}=a$ . Kita teruskan untuk suku ke-2, 3, hingga $n$ . ${\begin{aligned}a_{2}&=a+b\\a_{3}&=a+2b\\&\vdots \end{aligned}}$ Dengan memperhatikan pola, kita memperoleh $a_{n}=a+(n-1)b\quad \blacksquare$ .

Bukti

Kita mulai mengurutkannya dari suku

a_{1}=a

. Kita teruskan untuk suku ke-2, 3, hingga

n

{\begin{aligned}a_{2}&=a+b\\a_{3}&=a+2b\\&\vdots \end{aligned}}

Dengan memperhatikan pola, kita memperoleh $a_{n}=a+(n-1)b\quad \blacksquare$ .

Lebih umumnya, suku barisan ke- $n$ dapat ditulis

a_{n}=a_{m}+(n-m)b

dimana $m<n$ .

1. Beda

Beda, dalam suku barisan aritmetika, merupakan selisih dua suku. Misal $b$ adalah beda antar suku, secara matematis dapat ditulis sebagai berikut.

b=a_{n}-a_{n-1}

2. Suku Tengah

Suku tengah ialah suku yang berada di tengah-tengah barisan aritmetika jika banyaknya barisan suku berupa ganjil. Misal $a_{m}$ dan $a_{n}$ dengan $m<n$ mengapit sebanyak ganjil suku-suku lain dalam suatu barisan aritmetika. Karena itu, $n-m$ maupun $n+m$ adalah bilangan genap. Suku yang terletak antara $a_{m}$ dan $a_{n}$ adalah

a_{\frac {m+n}{2}}=a_{m}+\left({\frac {m+n}{2}}-m\right)b

dengan

b={\frac {a_{n}-a_{m}}{n-m}}

Kita dapat jabarkan lagi sehingga didapati:

a_{\frac {m+n}{2}}=a_{m}+\left({\frac {n-m}{2}}\right)\left({\frac {a_{n}-a_{m}}{n-m}}\right)={\frac {a_{m}+a_{n}}{2}}

Rumus Barisan dan Deret Aritmetika

Usai membahas pengertian singkat dari barisan dan deret aritmetika, pahami uraian tentang rumusnya berikut ini, dikutip buku berjudul Kumpulan Rumus Lengkap Matematika SMA/MA IPA/IPS karangan Khoe Yao Tung, berikut informasinya.

1. Rumus Barisan Aritmetika

Rumus untuk menentukan suku ke-n dari barisan aritmetika:

Un = a + (n – 1)b atau Un = Un-1 + b

Selain mencari rumus suku ke-n, adapun rumus yang digunakan untuk mencari nilai tengah dari sebuah barisan aritmetika, yakni:

Ut = ½ (a + Un)

Keterangan:
Un = suku ke-n
a = U1
Un-1 = suku sebelum suku ke-n
b = beda

2. Rumus Deret Aritmetika

Apabila dilihat secara sekilas, deret aritmetika memiliki komponen rumus yang sama dengan barisan aritmetika. Pembedanya adalah rumus barisan aritmetika digunakan untuk mencari suku yang diinginkan, sedangkan deret aritmetika mencari penjumlahan dari suku-suku tersebut.

Untuk lebih jelasnya, berikut rumus deret aritmetika, yakni:

Sn = n/2 (a + Un) = n/2(2a + (n – 1)b)

Berdasarkan rumus tersebut, dapat ditemukan suku ke-n dengan cara berikut ini, yaitu:

Un = Sn – Sn-1

Keterangan:
Un = suku ke-n
a = U1
Un-1 = suku sebelum suku ke-n
b = beda

Contoh Soal Barisan dan Deret Aritmetika

Supaya memahami lebih jelas tentang barisan dan deret aritmetika, simak terlebih dahulu contoh soalnya di bawah ini, seperti yang dikutip dari buku berjudul Isolasi Matematika SMP Kelas 1, 2, dan 3 karangan Herlik Wibowo.

Soal 1

Suatu bentuk deret aritmetika adalah 5, 15, 25, 35, …. Berapakah jumlah 10 suku pertama dari deret aritmetika tersebut?

Diketahui:

n = 10

U1 = a = 5

b = 15 – 5 = 25 – 15 = 10

Jawaban:

Sn = (2a + (n-1) b )

S10 = ( 2. 5 + (10 -1) 10)

= 5 ( 10 + 9.10)

= 5 x 100 = 500

Jadi, jumlah S10 dalam deret aritmetika tersebut, yakni 500.

Soal 2

Diketahui suatu deret aritmetika dengan suku pertamanya adalah 10 dan suku ke-enam adalah 20. Lalu, tentukan:

Beda deret aritmetika tersebut.

Tuliskan deret aritmetika tersebut.

Jumlah enam suku pertama dari deret aritmetika tersebut.

Jawaban:

Beda deret aritmetika tersebut, yaitu:

Un = a+(n-1)b

U6= a+(6-1) b

20= 10+(5)b

b= 10/5 = 2

Jadi, beda deret aritmetika tersebut adalah 2.

Deret aritmetikanya, yaitu:

10+12+14+16+18+20+…+Un

Jumlah suku keenam, S6 adalah:

Sn =n/2 (2a+(n-1) b)

S6= 6/2 (2.10+(6-1) 2)

=3(20+10)

=90

Jadi, jumlah suku keenam deret tersebut adalah 90.

Soal 3

Suku ke-40 dari barisan 7, 5, 3, 1, … adalah …

Diketahui:

a = 7

b = -2

Jawaban:

Un = a + (n – 1)b

U40 = 7 + (40-1)(-2)

= 7 + 39 . (-2)

= 7 + (-78)

= – 71

Jadi, suku ke-40 barisan aritmetika tersebut adalah –71.

Soal 4

Dalam suatu gedung pertunjukkan disusun kursi dengan baris paling depan terdiri atas 12 kursi, baris kedua berisi 14 kursi, baris ketiga berisi 16 kursi, dan seterusnya. Banyaknya kursi di baris ke-20 adalah …

Diketahui:

a = 12

b = 2

Jawaban:

Un = a + (n – 1)b

U20 = 12 + (20-1)2

= 12 + (9)2

= 12 + 38

= 50

Jadi, banyaknya kursi di baris ke-20 adalah sebanyak 50 kursi.

Soal 5

Seorang pegawai kecil menerima gaji tahun pertama sebesar Rp3.000.000,00. Setiap tahun gaji tersebut naik Rp500.000,00. Jumlah uang yang diterima pegawai tersebut selama sepuluh tahun adalah …

Diketahui:

Gaji pertama = a = Rp3.000.000,00

Kenaikan gaji tiap tahun = b = Rp.500.000

Gaji tahun kesepuluh = U10

Jumlah gaji selama sepuluh tahun = S10

Jawaban:

Un = a + (n – 1)b

U10 = 3.000.000 + (10 – 1)500.000

= 3.000.000 + (9 × 500.000)

= 3.000.000 + 4.500.000

= 7.500.000

Jadi, gaji pegawai yang didapatkan pada tahun kesepuluh adalah sebesar Rp 7.500.000,00

Soal 6

Hitunglah jumlah nilai suku ke-4 (S4) deret aritmetika apabila terdapat angka : 4, 8, 16, …?

Diketahui:

a = 4

b = 8-4 = 4

n = 4

Jawaban:

Un = a + (n-1) b

Un = 4 + (4-1)4

Un = 4 + 12

Un = 16

Lantas, berapa jumlah Sn?

Sn = 1/2 n ( a + Un )

S4 = 1/2 .4 (4 +16)

S4 = 4/2 (20)

S4 = 40

Jadi, jumlah nilai suku ke-5 pada deret aritmetika adalah 40.

Barisan dan deret geometri

Barisan & Deret Aritmetika dan Geometri – Pengertian, Rumus dan Contoh Soal

Mengenal apa itu barisan dan deret artimetika serta geometri, rumus lengkap, beserta contoh soalnya.

Sophia Maulidatul Adha

Tanggal diterbitkan3 Bulan Lalu

Photo by John Matychuk on Unsplash

Apakah kalian memperhatikan urutan bilangan yang dituliskan pada tempat parkir tersebut?

Berapa selisih urutannya?

Apakah semakin ke kanan urutannya semakin besar atau sebaliknya?

Betul sekali, Sobat! Penulisan bilangan pada tempat parkir tersebut membentuk sebuah barisan bilangan secara urut.

Sobat Pintar sudah pernah mendengar istilah barisan, bukan?

Barisan merupakan suatu runtutan angka atau bilangan dari kiri ke kanan dengan pola serta aturan tertentu. Barisan berkaitan erat dengan deret. Jika barisan adalah kelompok angka atau bilangan yang berurutan, deret merupakan jumlah dari suku-suku pada barisan. Barisan dan deret terbagi menjadi beberapa macam. Namun, kali ini kita hanya akan membahas mengenai barisan dan deret Aritmetika serta Geometri.

Yuk! Kita belajar bersama untuk mengenal barisan dan deret artimetika serta geometri lebih jauh lagi lewat artikel ini.

Barisan dan Deret Aritmetika

Sobat Pintar, pernah dengar istilah aritmetika?

Inget lho, ejaan yang benar adalah “aritmetika” bukan “aritmatika” ya!

Barisan dan Deret Aritmetika berbeda dengan aritmetika sosial, Sobat.

Misalkan seorang pedagang pada hari pertama jualan memperoleh untung sebesar Rp 10.000,-. Setiap harinya, untung yang diperoleh bertambah sebesar Rp 2000,-. Sehingga untung yang diperoleh pedagang tersebut dapat dituliskan dalam sebuah barisan artimetika berikut:

Rp 10.000, Rp 12.000, Rp 14.000, Rp 16.000, …

Barisan aritmetika merupakan barisan bilangan yang memiliki beda atau selisih tetap antara dua suku yang berurutan.

Contoh Barisan Aritmetika:

Rumus untuk menentukan suku ke-n dari barisan aritmetika:

Rumus untuk mencari beda pada barisan aritmetika:

Berbeda dengan barisan, deret merupakan hasil penjumlahan pada barisan aritmetika. Namun, deret tidak selalu menjumlahkan keseluruhan suku dalam suatu barisan. Rumus deret hanya menjumlahkan barisan aritmetikanya hanya sampai suku yang diperintahkan saja.

Contoh deret aritmetika:

2 + 4 + 6 + 8 + 10 + …

24 + 20 + 16 + 12 + …

Rumus jumlah n suku pertama deret aritmetika:

Contoh :

Diketahui sebuah barisan aritmetika 15, 19, 23, 27, 31, … .

a. Tentukan suku ke 25!

b. Tentukan 10 suku pertama!

Barisan dan Deret Geometri

Pernahkah Sobat Pintar mengamati bola yang sedang memantul?

Apakah kamu menyadari bahwa tinggi bola yang memantul semakin lama semakin rendah?

Nah, jika kita mendata tinggi pantulan bola, maka tingginya akan berurutan menjadi semakin rendah dengan rasio yang sama. Misalkan tinggi awal bola dijatuhkan adalah 4 meter, dan pantulan berikutnya adalah ½ dari tinggi sebelumnya, maka barisan geometri yang terbentuk, yaitu

Barisan geometri merupakan barisan bilangan dimana dua suku yang berurutan memiliki perbandingan yang sama. Perbandingan pada barisan geometri disebut sebagai rasio (r).

Contoh barisan geometri:

Rumus untuk menentukan suku ke-n dari barisan geometri:

Rumus untuk mencari rasio pada barisan geometri:

Deret geometri merupakan hasil penjumlahan pada barisan geometri. Rumus deret hanya menjumlahkan suku-suku pada barisan geometri hanya sampai suku yang diperintahkan saja.

Contoh deret geometri:

2 + 4 + 8 + 16 + 32 + …

200 + 100 + 50 + 25 + …

Rumus jumlah n suku pertama deret geometri:

Diketahui sebuah barisan geometri berikut:

3, 12, 48, 192, …

a. Tentukan suku ke-10 dari barisan geometri tersebut!

b. Tentukan jumlah 5 suku pertama dari barisan geometri tersebut!

Pembahasan:

Pengertian Bunga

Bunga yaitu selisih antara jumlah uang yang dipinjamkan oleh pemodal dengan jumlah uang yang akan dikembalikan oleh pemakai modal menurut kesepakatan bersama.

Adapun besarnya bunga dipengaruhi oleh: besarnya jumlah uang yang dipinjam, jangka waktu untuk meminjam, dan tingkat suku bunga / persentase. Bunga dibedakan menjadi 2 jenis, yakni bunga Tunggal dan bunga Majemuk. Berikut uraiannya..

Jenis-jenis Bunga

Berikut ini merupakan jenis-jenis bunga menurut besarnya bunga yang dibayarkan untuk setiap periode:

Bunga Tunggal

Bunga tunggal yaitu bunga yang dibayar untuk setiap periodenya dengan jumlah yang tetap. Bunga tunggal ini dihitung menurut modal awal.

Rumus bunga tunggal pada akhir periode;

$B=M_0\times t\times r$

Rumus besarnya modal pada akhir;

$M_t=M_0\times(1+t\times r)$

Keterangan:

B = bunga

M₀ = modal awal

M_t = modal pada akhir periode – t

t = periode

r = tingkat suku bunga (persentase)

Contoh soal

Sebuah lembaga koperasi simpan pinjam, memberikan bunga pinjaman untuk anggotanya sebanyak 2% per bulannya. Jika Nia meminjam uang sejumlah Rp. 800.000 dengan jangka waktu 4 bulan, tentukanlah besarnya bunga untuk setiap bulannya yang harus oleh Nia sesuai jangka waktu yang telah disepakati!

Jawab:

M₀ = Rp. 800.000

r = 2 %

t = 4 bulan

Sehingga, besarnya bunga untuk setiap bulan dihitung dengan:

$B=M_0\times t \times r$

$B=Rp.\, 800.000\times 1 \times 2%$

$B=Rp.\, 16.000$

dan jumlah uang yang harus dikembalikan setelah 4 bulan;

$M_t=M_0(1+t \times r)$

$M_4= Rp.\,800.000(1+4 \times2%)$

$M_4= Rp.\,800.000(1,08)$

$M_4= Rp.\,864.000$

lanjut ke…

Bunga majemuk

Bunga majemuk yaitu, bunga yang dihitung menurut jumlah modal yang dipakai ditambahkan dengan akumulasi bunga yang telah terjadi. bunga majemuk ini sering disebut dengan bunga berbunga, bunga majemuk dapat dihitung dengan menggunakan deret geometri.

Misalkan, Modal Sejumlah M0, akan diberlakukan bunga majemuk,dengan tingkat suku bunga i (dalam persentase) per periode waktu. Besarnya modal saat periode ke-t (Mt) bisa dihitung dengan cara:

Sehingga, rumus untuk besar modal pada periode ke-t dengan bunga majemuk yaitu;

keterangan;

Mt = modal pada akhir periode – t

M0 = modal awal

i = tingkat suku bunga

t = periode

Contoh soal

Sebuah bank swasta memberikan pinjaman kepada nasabahnya sebesar Rp. 6.000.000 dengan perhitungan bunga majemuk 3% per tahun. berapakah modal yang harus dikembalikan nasabah tersebut setelah 1 tahun?

Jawab:

M0 = Rp. 6.000.000

i = 3% = 0,03

Anuitas

Anuitas yaitu sistem pembayaran atau penerimaan secara berurutan dengan jumlah serta waktu yang tetap /tertentu. Apabila sebuah pinjaman dikembalikan secara anuitas, maka ada tiga hal yang menjadi dasar dari perhitungannya, yakni;

1. Besarnya pinjaman,

2. Besarnya bunga, dan

3, besarnya waktu serta jumlah periode pembayaran

Anuitas diberikan secara tetap untuk tiap akhir periode yang fungsinya membayar bunga atas hutang, dan mengangsur hutang itu sendiri, sehingga perhitungannya;

Anuitas = Bunga atas hutang + Angsuran hutang

Jika hutang sebesar M₀ = Memperoleh bunga sebesar b per bulannya dengan anuitas sebesar A, maka bisa ditentukan:

Besarnya bunga pada periode ke-n;

$B_n=(1+b)^{_{n-1}} (b\times M-A)+A$

Besar angsuran pada akhir periode ke-n: ditentukan dengan;

$A_n=(1+b)^{_{n-1}} (A-bM)$

dan sisa hutang pada akhir periode ke-n;

$M_n=(1+b)^n(M-\frac{A}{b})+\frac{A}{b}$

t = 12 bulan

Modal yang harus dikembalikan setelah 1 tahun /12 bulan yaitu:

Jawab:

P₀ = 100 gram

b = 3% = 0,03

$n=\frac{24}{4}=6$

Setelah 1 hari, maka ukuran radioaktif tersebut;

$P_n=P_0(1-b)^n$
$P_6=150(1-0,03)^6$

$P_6=150(0,97)^6$

$P_6=150(0,832)$

Peluruhan

Peluruhan yaitu berkurangnya nilai atau penurunan suatu besaran terhadap nilai besaran yang sebelumnya, yang umumnya mengikuti pola aritmatika (linier) atau geometri (eksponensial). Peluruhan misalnya, peluruhan zat radioaktif dan penurunan harga jual mobil.

Rumus peluruhan linear;

$P_n=P_0(1-n_b)$

Rumus peluruhan eksponensial;

$P_n=P_0(1-b)^n$

Keterangan;

P_n = nilai besaran setelah n periode

P₀ = nilai besaran pada awal periode

b = tingkat peluruhan

n = banyaknya periode pertumbuhan

Contoh Soal

Sebuah bahan radioaktif, mulanya berukuran 150 gram mengalami reaksi kimia sehingga mengalami penyusutan sebanyak 3% dari ukuran sebelumnya setiap 4 jam secara eksponensial. Tentukanlah ukuran bahan radioaktif tersebut setelah 1 hari!

Jawab:

P₀ = 100 gram

b = 3% = 0,03

$n=\frac{24}{4}=6$

Setelah 1 hari, maka ukuran radioaktif tersebut;

$P_n=P_0(1-b)^n$
$P_6=150(1-0,03)^6$

$P_6=150(0,97)^6$

$P_6=150(0,832)$

$P_6=124,8 gram$

Bunga Anuitas Adalah

Anuitas merupakan pembayaran yang dilakukan pada interval tetap. Sumber: Simplilearn

Bunga anuitas adalah metode perhitungan bunga yang mengatur jumlah angsuran pokok, ditambah angsuran bunga yang dibayar agar sama setiap bulannya. Dilansir dari situs resmi OJK, dijelaskan bahwa pada perhitungan anuitas, porsi bunga pada masa awal akan sangat besar sedangkan porsi angsuran pokok sangat kecil. Mendekati berakhirnya masa kredit, keadaan akan menjadi berbalik. porsi angsuran pokok akan sangat besar sedangkan porsi bunga menjadi lebih kecil. Lebih jelasnya Anda bisa melihat gambar di bawah ini:

Pada penjelasan gambar di atas, dapat dilihat bahwa di 1-2 tahun pertama, cicilan per bulan lebih banyak dialokasikan untuk membayar bunga yang ditandai warna merah. Sedangkan pinjaman pokok yang ditandai warna kuning, alokasi pembayarannya lebih sedikit. Untuk mengetahui lebih jelasnya, selanjutnya akan dibahas bagaimana cara menghitung bunga anuitas tersebut serta simulasinya.

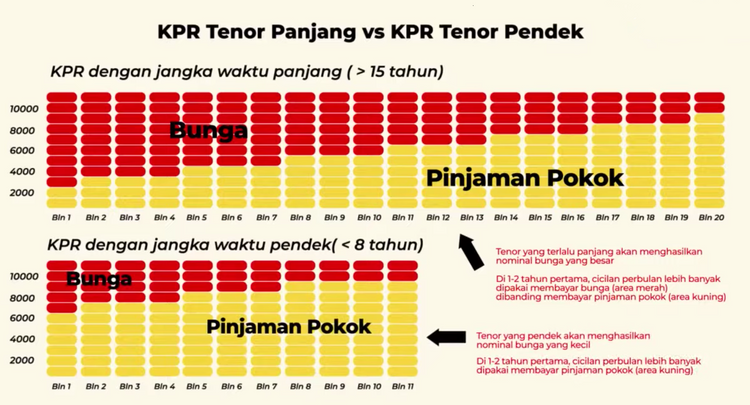
Rumus Menghitung Bunga Anuitas

Sederhananya, bunga anuitas membuat jumlah angsuran setiap bulan sama. Sumber: Pixabay

Mengutip Sikapi Uangmu OJK, metode menghitung bunga anuitas mengatur jumlah angsuran pokok ditambah angsuran bunga yang dibayar agar sama setiap bulan. Dalam perhitungan bunga anuitas, porsi bunga pada masa awal sangat besar sedangkan porsi angsuran pokok sangat kecil. Mendekati berakhirnya masa kredit, keadaan akan menjadi berbalik. porsi angsuran pokok akan sangat besar sedangkan porsi bunga menjadi lebih kecil.

Sistem bunga anuitas ini biasanya diterapkan untuk pinjaman jangka panjang semisal KPR atau kredit investasi. Untuk menghitung angsuran dengan bunga anuitas secara manual, Amda bisa menerapkan rumus yang digunakan dalam menghitung bunga efektif. Rumus yang digunakan adalah sebagai berikut:

Bunga = SP x i x (30/360)

Keterangan:

SP adalah saldo pokok pinjaman di bulan sebelumnya
I adalah suku bunga per tahun
30 adalah jumlah hari dalam sebulan
360 adalah jumlah hari dalam setahun

Namun, rumus ini dikembangkan lagi untuk mendapatkan nilai yang sesuai berdasarkan rumus anuitas menjadi:

P x i x [(1+i)xt) / (1+i)t-1)]

Keterangan:

P adalah pokok pinjaman
i adalah suku bunga
t adalah periode kredit

Pembayaran Pokok

987.224

Pembayaran Bunga

67.767

Jumlah Angsuran

1.054.991

Sisa Pokok

7.144.798

Sisa Utang

7.144.798

Pembayaran Pokok

995.451

Pembayaran Bunga

59.540

Jumlah Angsuran

1.054.991

Sisa Pokok

6.149.348

Sisa Utang

6.149.348

Pembayaran Pokok

1.003.746

Pembayaran Bunga

51.245

Jumlah Angsuran

1.054.991

Sisa Pokok

5.145.602

Sebelum menghitung semua, pastikan sudah menghitung besaran bunga anuitas seperti di atas. Selain itu, pastikan bahwa jumlah angsuran selalu sama, sehingga terlihat pokok angsuran semakin membesar, sedangkan bunga pinjaman semakin mengecil.

Sisa Utang

12.000.000

Pembayaran Pokok

954.991

Pembayaran Bunga

100.000

Jumlah Angsuran

1.054.991

Sisa Pokok

11.045.009

Sisa Utang

11.045.009

Pembayaran Pokok

962.946

Pembayaran Bunga

92.042

Jumlah Angsuran

1.054.991

Sisa Pokok

10.082.060

Sisa Utang

10.082.060

Pembayaran Pokok

970.973

Pembayaran Bunga

84.017

Jumlah Angsuran

1.054.991

Sisa Pokok

9.111.087

Sisa Utang

9.111.087

Pembayaran Pokok

979.065

Pembayaran Bunga

75.926

Jumlah Angsuran

1.054.991

Sisa Pokok

8.132.022

Sisa Utang

8.132.022

Pembayaran Pokok

987.224

Pembayaran Bunga

67.767

Jumlah Angsuran

1.054.991

Sisa Pokok

7.144.798

Jenis-Jenis Bunga Anuitas

Jika Anda melakukan pembayaran pinjaman secara teratur, nilai masa depan berguna dalam menentukan total biaya pinjaman. Sumber: Pinterest

Dengan menghitung bunga anuitas ada beberapa komponen yang dipertmbangkan yakni nilai masa depan dan nilai sekarang. Nilai masa depan adalah ukuran berapa banyak serangkaian pembayaran reguler akan bernilai di beberapa titik di masa depan, dengan tingkat bunga tertentu.

Kalau Anda berencana untuk menginvestasikan jumlah tertentu setiap bulan atau tahun bisa memberitahu Anda berapa banyak diakumulasikan di masa mendatang. Jadi, kalau Anda melakukan pembayaran pinjaman secara teratur, nilai masa depan berguna dalam menentukan total biaya pinjaman.

Berbeda dengan perhitungan nilai masa depan, perhitungan nilai sekarang bisa membantu Anda mengetahui berapa banyak uang yang akan dibutuhkan sekarang untuk menghasilkan serangkaian pembayaran di masa depan, sekali lagi dengan asumsi tingkat bunga yang ditetapkan.

1. Anuitas Jatuh Tempo

Dengan anuitas jatuh tempo, sebaliknya, pembayaran datang pada awal setiap periode. Contoh pembayaran jatuh tempo anuitas termasuk sewa, sewa, dan pembayaran asuransi, yang dilakukan untuk menutupi layanan yang diberikan pada periode setelah pembayaran.

Ringkasnya, pembayaran pertama diterima pada awal periode pertama, dan setelah itu, pada awal setiap periode berikutnya. Pembayaran untuk periode terakhir, yaitu periode x diterima pada awal periode x untuk menyelesaikan total pembayaran yang jatuh tempo.

2. Anuitas Langsung

Anuitas ini memakai metode pembayaran atau penerimaan cicilan secara berkala pada jangka waktu tertentu dan dilakukan secara langsung tanpa penundaan waktu atau tempo seperti pada pembayaran kredit barang. Anuitas langsung adalah jenis anuitas paling dasar dengan satu kontribusi sekaligus. Ini karena diubah menjadi aliran pendapatan yang berkelanjutan dan terjamin untuk jangka waktu tertentu (sedikitnya lima tahun) atau seumur hidup. Penarikan dapat dimulai dalam waktu satu tahun.

3. Anuitas Sederhana

Anuitas biasa membuat (atau membutuhkan) pembayaran pada akhir setiap periode. Misalnya, obligasi umumnya membayar bunga pada akhir setiap 6 bulan.

4. Anuitas Tertunda

Anuitas yang ditangguhkan dapat datang dengan segala macam fitur dengan biaya yang memberikan beberapa jenis manfaat kematian dan/atau jaminan pendapatan di masa depan. Pembayaran atau penerimaan cicilan anuitas tangguhan dilakukan secara berkala pada jangka waktu tertentu atau dilakukan setelah beberapa periode berjalan seperti anuitas pada bunga deposito dan bunga pinjaman.

Bunga anuitas adalah modifikasi dari perhitungan kredit bunga efektif. Nah, bagi Anda yang sedang cari rumah di lokasi yang strategis namun harganya cukup terjangkau hingga cicilannya tidak terlalu besar

Kelebihan dan Kekurangan Bunga Anuitas

Jika ingin meminjam bunga anuitas, sebaiknya pertimbangkan dua sisi yaitu kelebihan dan kekurangannya. Sumber: Pinterest

Meski terkesan seperti bunga tetap yaitu angsuran setiap bulan sama, namun bunga anuitas merupakan pengembangan dari bunga efektif memiliki kelebihan dan kekurangan yang bakal diketahui kedua belah pihak dalam pinjam-meminjam, terutama nasabah.

Kalau Anda ingin meminjam dan ditawarkan penggunaan bunga anuitas, sebaiknya pertimbangkan dua sisi yaitu kelebihan dan kekurangannya. Berikut ini penjelasan mengenai dua sisi dari penerapan bunga anuitas tersebut.

Kelebihan	Kekurangan
Angsuran bulanan yang dibayarkan tetap, sehingga tidak memengaruhi arus kas.	Penghitungan rumit karena lebih sulit dihitung manual sehingga disarankan menggunakan software.
Bunga dihitung secara jelas yaitu dari sisa pokok yang belum dibayar.	Meski jumlah cicilan sama setiap bulan, yang kita bayarkan atau dilunasi lebih dulu adalah bunga pinjaman. Sehingga, pokok pinjaman yang dibayarkan semakin besar hingga akhir masa pengembalian pinjaman.
Tidak merepotkan bagi peminjam yang harus terus menghitung sisa pokok pinjaman seperti dalam pinjaman dengan bunga efektif.

Cari Blog Ini

BagasWahyuPrasetyo _X IPS 1